Точка Нагеля и сложная задача

Целью этой статьи является наглядно показать ученикам и учителям широту спектра рассматриваемых тем для конкурентноспособного участия в различных Олимпиадах и при поступлении в вузы на примере решения одной задачи:
Построить треугольник (с помощью циркуля и линейки) по точке Нагеля, вершине B и основанию высоты, опущенной из этой вершины. (К. Кадыров, Украина, 8-9 кл)
Для решения этой задачи необходимо ознакомиться с определением точки Нагеля, а также с теоремами, которых нет в образовательных программах многих стран.
Точка Нагеля – точка пересечения отрезков, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями.
Теорема о существовании точки Нагеля (1)
Необходимо доказать, что отрезки, соединяющие вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями пересекаются в одной точке

Доказательство:
Обозначим |AK|=m,|CK|=n,|CL|=s,|BL|=q,|AM|=d,|BM|=l.
Отрезки |CF|=|CG|, т.к отрезки касательных выходящих из одной точки равны. По той же причине |AF|= |AM|=d и |BG|=|BM|=l. Тогда
|??|=?+?+? и |??|=?+?+?, следовательно, ?+?+?= ?+?+?=?, где ? – полупериметр. Тогда ?=|??|−|??|=?−?. По аналогии ?=?−?,?=?−?,?=?−?,?=?−?,?=?−?.
Используя теорему Чевы доказываем существование точки Нагеля ?−??−?∙?−??−?∙?−??−?=1
Теорема доказана.
В любом треугольнике его точка Нагеля N, центроид G, и центр вписанной окружности I лежат на одной прямой, причем ????=?? (точка G лежит внутри отрезка NI) (теорема 2). (рис.2)
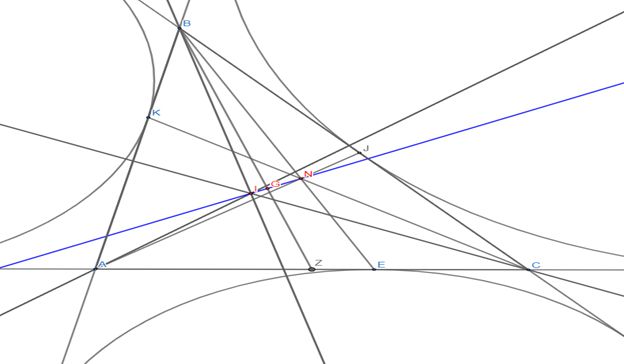
Для доказательства достаточно убедиться в том, что гомотетия ??−12 с центром в точке пересечения медиан и коэффициентом ?=−12 переводит точку Нагеля в центр вписанной окружности (рис.3)
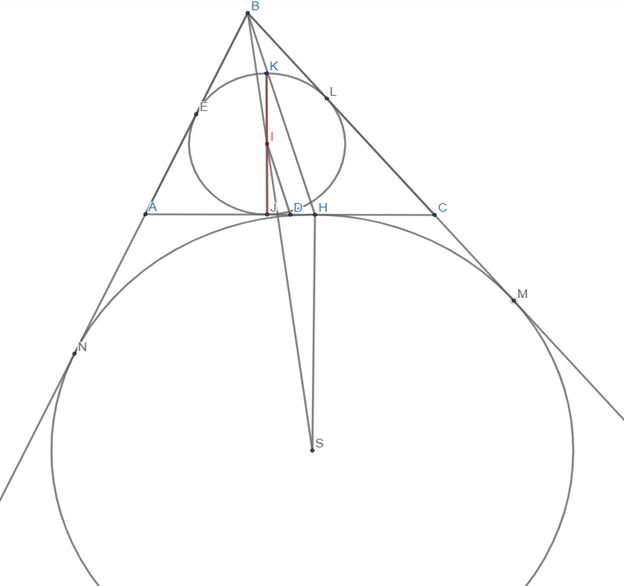
Другими словами, достаточно показать, что прямая, соединяющая точку B c cоответствующей точкой касания вневписанной окружности H перейдет в прямую, проходящую через центр вписанной окружности I. Таким образом, образ нашей прямой есть некоторая прямая, проходящая через середину стороны AC – точку D (данная гомотетия переводит вершину треугольника в середину противолежащей стороны), причем параллельно исходной прямой.
(образ прямой, не проходящей через центр гомотетии есть параллельная ей прямая).
Также прямая, соединяющая вершину треугольника B с точкой H касания вневписанной окружности со стороной AC, проходит через точку K, диаметрально противоположную точке J касания вписанной окружности со стороной AC (т.е. симметричную ей относительно центра вписанной окружности) – что сразу следует из рассмотрения гомотетии с центром в B,
переводящей вписанную окружность во вневписанную: точка K переходит в точку H.
Заключаем, что образ прямой есть средняя линия ID в треугольнике KHJ (точки касания вписанной и описанной окружности со стороной AС симметричны относительно ее середины), и потому проходит через центр вписанной окружности.
После ознакомления с новым материалом можно приступить к решению основной задачи.
I – инцентр треугольника ABC (центр вписанной окружности)
G – центроид (точка пересечения медиан)
N – точка Нагеля
rb – радиус вневписанной окружности, соответвующей вершине B
r – радиус вписанной окружности
p – полупериметр треугольника ABC
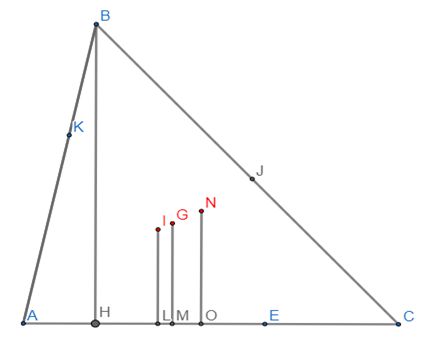
Из условия сразу определяются длина отрезка BH (высота треугольника), прямая AC, длина отрезка NO. Введем обозначения: |??|=ℎ, |??|=?. (рис.4)
Длина отрезка |??|=ℎ3 (почему?) Отсюда можем вычислить длину радиуса вписанной окружности |IL|. Для этого рассмотрим прямоугольную трапецию INOL. Применяя теорему 2 и подобие определяем 1ℎ3−|??|=3?−|??| →|??|=12(ℎ−?).
Далее воспользуемся формулами определения площади треугольника для нахождения длины радиуса вневписанной окружности. ?=12?∙ℎ=?∙?=??∙(?−?)
Выражая полупериметр получаем ?=??∙???−?→??=ℎ?ℎ−2?.
Для того чтобы найти длину ?? предлагаю решить следующую задачу на построение: Зная длины отрезков a, b, c найдите длину отрезка ???
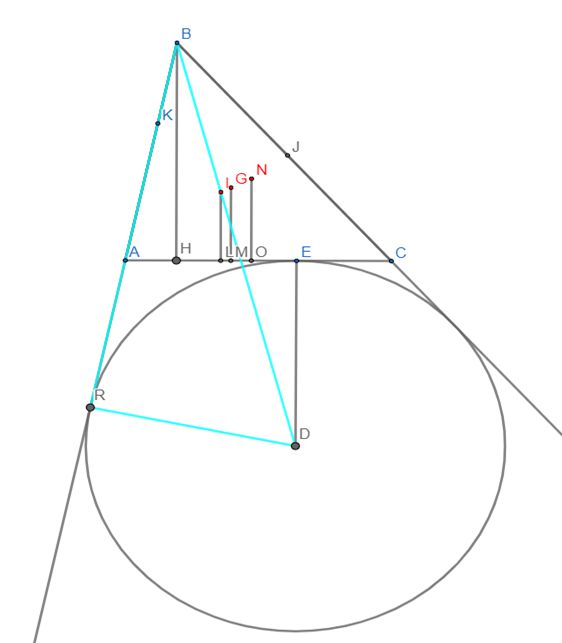
Осталось определить вершины A и C (рисунок 5). Для этого воспользуемся тем, что треугольник BRD является прямоугольным. В нем известны длины отрезков |DR|=?? и |BD|, т.к. местоположения точек B и D уже определены. Аналогично определяем точку C. Построение завершено.
В заключение хочется отметить, что эта задача была найдена в материалах Олимпиады по геометрии имени Шарыгина заочного этапа. Ученикам следует участвовать в такого рода Олимпиадах, т.к. в них можно почерпнуть много полезного, чего не проходят на уроках. Также читатель мог заметить, что теоремы Чевы так же нет в школьном курсе, ее проходят в классах с углубленным изучением математики. Формула для вычисления площади через радиус вневписанной окружности встречается в материалах ЕГЭ и олимпиадах для поступления в российские вузы.
Руслан АРКАБАЕВ
Загрузка...