Математикадағы ақырсыз кіші шамалар жайында толғансақ
ХVII ғасырдың екінші жартысында математика әлеміндегі ең ірі төңкерілістердің бірі жүзеге асты. Әйгілі Ньютон мен Лейбництің арқасында адамзат интегралдау мен дифферениалдау амалдарына қол жеткізді. Бұрын соңды мүмкін емес деп танылған есептеулер жаңа математикалық аппараттар арқасында жүзеге асырылатын болды. Қозғалып бара жатқан денені зерттеу үшін таптырмас құралға айналған жаңа апараттар математикалық анализді дүниеге әкелді.

Ньютонның 1687 жылы жарық көрген «Табиғи философияның математикалық бастамалары» және Лейбництің 1684 жылы жарық көрген «Максимумдар мен минимумдардың жаңа әдісі» атты еңбектері ғылым дамуының жаңа легін тудырды. Математиктер мен мен физиктер ақырсыз аз және ақырсыз үлкен шамалармен жұмыс істеу құралын меңгере бастады. Ақырсыз аз шамалар және ақырсыз үлкен шамалар ұлылар ойын ерте заманда-ақ алаңдата бастаған болатын. Біздің заманымыздан бұрынғы V-IV ғасырларда өмір сүрген гректің ұлы философтарының бірі Платон өз еңбектерінде келесі ой қалдырған екен. Егер «2» саны жоқ болса «1» санының мағынасы жоқ, сол сияқты кез келген «n» санының мағынасы бар болу үшін «n+1» санының да болуы қажет.
Яғни натурал сандар қатары шексіз үлкен, шексіз көп саннан тұрады. Сондай ақ, біз «1», «2» . . . деп санау барысында бір мен екінің арасында шексіз көп сан бар екенін ескермейміз. Мысалы секілді дұрыс бөлшектер саны шексіз көп және олардың барлығы барлығы «0» мен «1» арасында орналасқандығы белгілі, ал түріндегі бөлшектердің барлығы бір мен екі арасында орналасқан. Демек, 1 мен 2 сандарының арасында шексіз көп сан орналасқан. Бұл философиялық ой кейіннен математикаға «рационал сандардың тығыздығы туралы теорема» деген атпен енді. Грек ойшылдарының ең табысты кезеңі болып саналатын дәуірде шексіз үлкен және шексіз аз шамалар жайлы өз ойларын Платоннан бастап, Евдокс, Евклид, Зенон, Вавилондық Диаген сынды ойшылдар да қалтырған. Алайда бұл мәселеде аталған ойшылдардың ізін қостап, Евклидтің еңбектерін оқып өскен Архимедтің орны ерекше.
Жоғары аталған ойшылдардан өзгеше ойланатын Архимед теория мен практиканы қатар ұстанған болатын. Жан тәні жаңаның бәрін меңгеруге дайын болған Архимед ерте дәуірде өмір сүрсе де, қазіргі ғылымдардың көпшілігінің шет-жағасын меңгеріп кеткен. Механика, физика, геометрия, инженерия сынды ғылымдарды жаңа деңгейге көтерген ұлы ойшыл, интегралдау идеясын да қалыптастырып кеткен. Лейбниц өз еңбегін «Максимумдар мен минимумдардың жаңа әдісі» деп атағанымен, негізгі идеясы Архимедтің ойлап тапқанынан алысқа кеткен жоқ. Бәлкім Лейбництің «Архимедтің еңбектерін оқи отырсаң, геометрлардың кейінгі жетістіктеріне таң қалмайсың» деуі бекер емес шығар. Осы жерде «интегралдау» сөзінің мағынасын ашып айту керек: Интегралдау сөзі терең математикалық анықтамасына тоқталмай, қарапайым тілмен айтқанда – шексіз көп шексіз кіші шамалардың қосындысы. Архимед шеңбер ұзындығының оның диаметріне қатынасын іздеу барысда дәл осы интегралдау әдісін қолданған. Өз заманы үшін мүлдем қол жетімсіз болып көрінген, (Пи, 3,14…) санын 99,99% пайызға дейінгі ділдікпен анықтаған және санын есептеудің математикалық әдісін көрсеткен алғашқы адам болып саналады. Осы математикалық әдіс негізінде біз қарастырған «интегралдау» болып табылады.
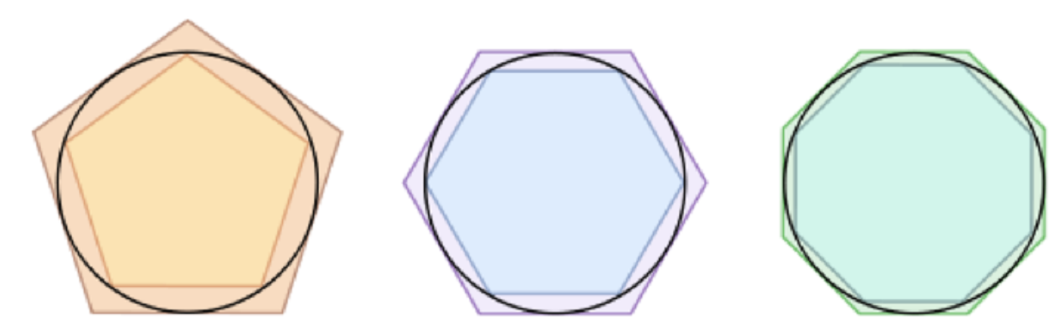
Осы әдісіне тоқталайық. Архмед келесі заңдылықты байқады: «Егер шеңберге іштей және сырттай дұрыс алтыбұрыш салынса, шеңбер ұзындығы іштей салынған атыбұрыш периметрінен үлкен, ал сырттай сызылған алтыбұрыш периметрінен кіші. Алтыбұрыш орнына жетібұрыш салса, осы заңдылық сақталады, бірақ екі периметр бір біріне жақындайды, сегіз бұрышта да…». Осылайша Архимед радиусы 1-ге тең болатын шеңберге іштей және сырттай сызылған дұрыс 96-бұрышқа дейін қарастырады. Осы сәтте дұрыс көпбұрыштардың қабырғалары өте кішкентей шамаға айналып, ұзындықтары бір біріне жақындайды, ал көп бұрыштардың өздері шеңберге ұқсап кетеді.
Архимед өзінің стериометрияға арналған «Көпжақтар туралы» атты еңбегінде пирамида көлемін анықтауға арналған формуланы қорытып шығарған. Ол үшін тағы да интегралдау әдісін қолданады. Осы бағытта ойшыл келесі ой қортындыларды пайдаланады: кез келген пирамиданы үшбұрышты пирамидаларға бөлуге болады; кез келген үш бұрышты пирамиданы екі призмамен екі үш бұрышты приамидаға бөлуге болады. Осы екі лемманы алға қоя отырып, Архимед кез келген пирамиданы шексіз көп призмалардың қосындысы түрінде жазуға болатынын дәлелдеді. Призманың көлемін табу шешілген мәселе болғандықтан, пирамиданың да көлемін таба алатыны айқын болды. Есептеулер нәтижесінде Архимед пирамида көлемі туралы теореманы дәлелдеді.
Осылайша ХVII ғасырда математика әлемін шулатқан еңбектердің түп негізінде ертенің ойшылдарында пайда болған идеялар жатыр. Сондықтан да математика ерекше ғылым болып саналады, мейлі 100 жыл мейлі 1000 жыл, тіпті 2500 жыл бұрын математикалық жолмен дәлелденген теорема ешқашан да өз күшін жоймайды. Жаңа технология дамыса да, жаңа гипотезалар құрылса да, математиканың ең бірінші теоремалары мен аксеомалары өзектілігін жоғалтпайды. Осындай ерекшелігімен басқа еш-бір ғылым мақтана алмайды.
Нұрғазы ТҰРСЫНҒАЗИН,
Семей қаласындағы физика – математика
бағытындағы Назарбаев Зияткерлік мектебінің
математика пәнінің мұғалімі, Шығыс Қазақстан облысы